Introduction
One question that bothers our mind when we read positional encoding is whether it helps the model or not. It is observed that adding position embeddings only helps marginally in a convolutional neural network as CNN uses relative position embedding (implicitly). It is not the case for transformers as the model is permutation invariant without positional information added to the input embeddings. It is also empirically observed that removing positional embeddings (in the transformer architecture) altogether hurts the performance (with certain exceptions like NoPE).
Whenever one reads about positional encoding scheme, one may ask the following questions to understand it better
- Absolute or relative?
- Fixed (deterministic) or learnable?
- Injected only at the input block (layer) or all the blocks?
- Inductive or not-inductive (BERT, RoBERTa)?
Notations
We will closely follow the standard notations:
- Embedding matrix: $ E \in \mathbb{R}^{len(vocab)} \times d_{model}$
- Token embeddings : $ X \in \mathbb{R}^{n \times d_{model}}$
- Absolute Position embeddings: $P \in \mathbb{R}^{n \times d_{model}}$
- Input to Transformer: $X+P \in \mathbb{R}^{n \times d_{model}}$, $n$ is the length of the sequence
- Projection matrices: $W_Q,W_K,W_V \in \mathbb{R}^{d_{model} \times d_k}, \quad d_q=d_k=d_v$
- Context window size: $n_{max}$
Absolute Position Encoding
In absolute position encoding, we add the position information to the input embeddings. The position is also a sequence [1,2,3,4,…,n]. Mathematically, we say it is simply a progression (arithmetic or geometric). However, to find the $t$-th position in the progression, we need the first position. That is why it is called absolute position encoding (ape). The embeddings of the positions can be fixed or learnable.
We have the input matrix $X$ and the position matrix $P$ (fixed or learnable) of the same size. Then the input to the transformer is an elementwise addition of these two matrices. Decomposing the pre-attention $A_{pre}$ matrix provides a better insight into how the positional information is being used by the model
$$ \begin{aligned} A_{pre} = QK^T &= (X+P)W_Q W_K^T(X+P)^T=(XW_Q+PW_Q)(W_K^TX^T+W_K^TP^T) \\ & = XW_QW_K^TX^T+PW_QW_K^TX^T+XW_QW_K^TP^T+PW_QW_K^TP^T \end{aligned} $$
The pre-attention score is the sum of 4 terms all involving dot products between the words (the first term), between the positions (the last term) and between the words and positions (2nd and third term). It is reasonable as we expect it to take the position into account while attending to words in a sentence. Therefore, the model is no longer permutation-invariant.
Fixed Position Encoding
The original transformer architecture followed the fixed sinusoidal embedding. Suppose the embedding dimension $d_{model}=512$, then $j=0,1,2,\cdots,255$. Then each position embedding is a geometric progression of the wavelength of the sinusoid starting from $2 \pi$ (for $j=0$) to $10000 \cdot 2 \pi$ (for $j=255$),
$$P(pos,2j)=sin(\frac{pos}{10000^{2j/d_{model}}})$$ $$P(pos,2j+1)=cos(\frac{pos}{10000^{2j/d_{model}}})$$
Either one can concatenate or interleave these positions to get the final position embedding. This particular formulation has many possible interpretations. I have written a detailed article on medium. As mentioned in the paper, for any fixed offset $k$, $P(pos+k)$ can be represented as a linear function of $P(pos)$.For example,
Consider a sentence: “A cat is smaller than an elephant”
Shift the sentence by $k=2$ units: “ You know, a cat is smaller than an elephant”
Suppose the $P_4 \in \mathbb{R}^{1 \times 512}$ be a positional embedding for the second position (for the word “smaller”) in the first sentence, then $P_{4}=P_1W$ or $P_{4}=P_3W$ or $P_{4}=P_iW$ (Proof). That is, one can get the positional embedding for a particular position as a linear function of other position embedding. Therefore, the model learns to attend to the relative positions as well. However, how effectively it learns the relative position is a different question (answer: not effective) and it is addressed by Shaw in their paper on relative positions
Learnable
The same transformer paper also used learned absolute position embeddings by randomly initializing the position embeddings. However, in terms of performance, both fixed and learned embeddings gave the same level of performance. So going with the fixed embedding saves some computational budget.
Improvements: FLOATER transformer generalizes the sinusoidal PE under the continuous dynamic models. They argued that any PE scheme should be Inductive ( handle sequences longer than any sequence seen in the training time), Data-Driven(learnable from data) and Parameter-efficient
Drawbacks
- Despite having the ability to get the embedding for a new position, the performance degrades during inference if it goes beyond the context length (because the model was not trained on the embedding of the new position).
Shortformer
One important observation from the above decomposition is that one can add positional information directly in the attention layer as well!. The advantages are two-fold
- Adding it directly to the input embedding is non-trivial due to $n$ possible encodings for each token
- The dimension of embedding should of $d_{model}$ if added directly, whereas adding it in attention is $d_k$.
Shortformer follows this approach by adding positional information (learnable) at the queries and keys but not in values as shown below
$$ \begin{aligned} A_{pre} = QK^T &= (X+P)W_Q \quad W_K^T(X+P)^T \\ A &= Softmax(A_{pre})V \end{aligned} $$
Relative Position Encoding
The relative position plays a role when the relative positions in a sentence matter and makes sense in the real world. For example, “the cat eats cheese” makes more sense than “the cheese eats cat” (though grammatically correct). We expect the model to learn relative positions just from the absolute positions is good but may not be efficient Often in practice, a relative position encoding scheme is used in addition to the absolute position encoding. However, the relative position of a word in a given sentence of length $n$ has $n$ possible values. It is not necessary to measure the relative position with respect to all other words in a sentence. We may limit it to $k$ words. How do we add a learnable relative position embedding?
Let us re-write the $A_pre$ decomposition equation for a single element in the pre-attention matrix and add a learnable vector $r_{j-i} \in \mathbb{R}^{d_k}$ that learns the relative position $j-i$.
$$ \begin{aligned} A_{pre}[i,j] = \frac{((x_i+p_i)W_Q)((x_j+p_j)W_K+r_{j-i})^T}{\sqrt{d_k}} \end{aligned} $$
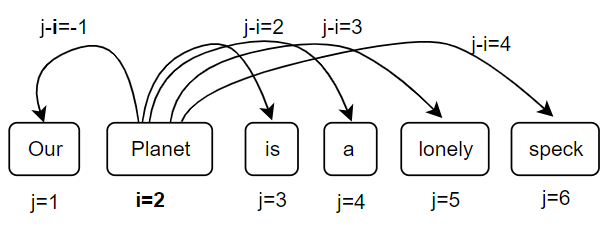
This essentially translates to learning the relative position between the key vector and the query vector (it is also ok to add it to the value vector). One can think of $r_{j-i}$ as adding the inductive bias. In practice, we do not need to compute the relative position of a word to all other words in the sentence. We may limit it to $\pm k$ words. Therefore, the embedding matrix for the relative position is also fixed.
$$ \begin{aligned} A_{pre}[i,j] = \frac{((x_i+p_i)W_Q)((x_jW_K+p_jW_K+r_{j-i})^T}{\sqrt{d_k}} \end{aligned} $$
Illustration
Suppose we have a transformer with a context length $n=20$, and the max-relative position length $k=4$ ($2k+1=9$ if the relation is bidirectional as shown in the figure). Then the absolute position embedding matrix would be of size $20 \times d_{model}$, and the relative position embedding matrix $P_r$ would be of size $9 \times d_k$. What if $(j-i>abs(k))$, for example, $i=2,j=12$? Simply limit it to the upper/lower bound ($k=\pm 4$). Mathematically, $max(-k,min(k,j-i))$.
Note: Relative positions are added separately in the attention sub-layer of all the layers. This is not required for APE as it propagates to all the layers along with the input representations.
T5 Variation
Observe that adding the relative positional info as a learnable vector $(\in \mathbb{R}^{d_k})$ to the key vector ultimately affects the attention score which is a scalar ($\in \mathbb{R}$). Then why don’t we add this scalar directly to the attention score as a learnable parameter? This reduces the number of learnable parameters significantly. This is what exactly followed in the T5 model,
$$ \begin{aligned} A_{pre}[i,j] = \frac{((x_i+p_i)W_Q)((x_j+p_j)W_K)^T}{\sqrt{d_k}}+b_{j-1} \end{aligned} $$
where $b_{j-1} \in \mathbb{R}$ that is shared across heads and layers.
Transformer-XL variation
Transformer-XL tackles the problem of training longer sequences by introducing recurrence in the hidden states of all the layers. In such a case, using absolute position encoding is not trivial. Therefore, they used RPE with the following modifications
$$ \begin{aligned} A_{pre}[i,j] = x_iW_QW_{K1}^Tx_j^T+x_iW_QW_{K2}^Tr_{i-j}^T+u W_{K1}^Tx_j^T+vW_{K2}^Tr_{i-j}^T \end{aligned} $$
Where the common $W_K$ matrix in the original decomposition is re-parameterized to $W_{K1}$ and $W_{K2}$, new parameter vectors $u,v$ that are independent of the query position were introduced. Finally, the relative position $r_{i-j}$ (uses the sinusoidal function for embedding matrix) is used.
RoPE
It stands for Rotary Position Embeddings. The diagram below shows the vector representation of the position embeddings (in the 2d case) for the first 7 positions. The relative distance as measured (in angles) between $pos=0$ and $pos=1$ are the same for any two positions.
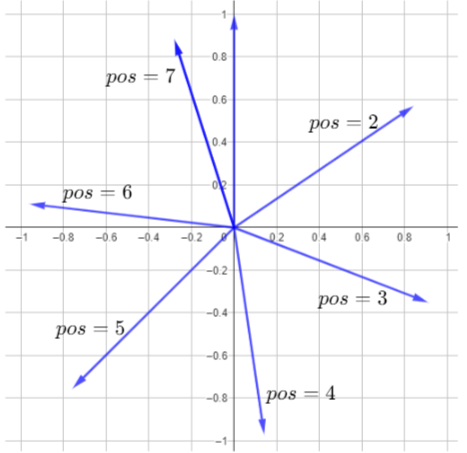
Will that be the case if we consider the last two dimensions (511,512)?. The RoPE proposes to use the rotation matrix in the attention head applied to queries and keys. It rotates two consecutive elements in the word embedding vector by using a Block rotation matrix shown below
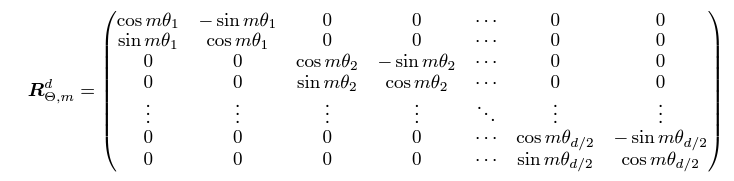
where $m$ is the position index and $\theta_i=10000^{(2-i)/d},i=1,2,\cdots, \frac{d}{2}$. Then the final query-key attention is given by
$$ q_m^Tk_n=(R_{\Theta,m}^d W_qx_m)^T(R_{\Theta,n}^dW_kx_n) $$
You may watch this video for intuitive explanations
ALiBi
Handling sequences larger than the model was trained on using Attention with Linear Bias (ALiBi). The idea is very simple. Just add a bias (hand-crafted) after the query-key product as shown below
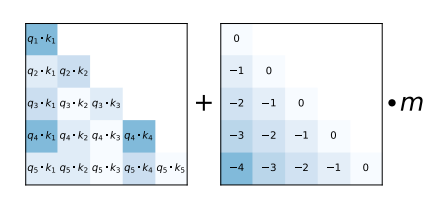
Interesting question: how does a model achieve extrapolation at inference time for sequences that are longer than it saw during training?
Surprising Result: We show that using ALiBi trains a 1.3 billion parameter model on input sequences of length 1024 that extrapolates to input sequences of length 2048, achieving the same perplexity as a sinusoidal position embedding model trained on inputs of length 2048 but training 11% faster and using 11% less memory
NoPE
How about generalization to downstream tasks? None of the PEs (APE,RPE,RoPE,ALiBI) extrapolate the sequence length when adapted for downstream tasks. The causal attention mask provides some notion of the absolute position of the words. It is argued the postional information is learned by the first hidden layer of the self-attention layers. So, No Positional Encoding (NoPE) is required.
To do
Add illustrations, and recent paper xPOS, Is adding positional information for special tokens necessary? How useful it is? TUPE